This post is about introducing ARIMA using the CPI data and various R framework for time series. Autoregressive because it is based on past value and moving average to smooth the time series data. Our previous post on autocorrelation and partial autocorelation could be considered as prior material. The assumption behind these models are that the time-series is stationary (or has been transformed to a stationary time series). Recall that a stationary time series has constant mean, variance and auto-correlation over time. In other words, the covariance between the i-th term and the i + m - th term is not a function of time.
Autoregression is a class of linear model where the outcome variable is regressed on its previous values (lagged observations).
\[Y_t = \delta + \phi_1 Y_{t-1} + \phi_2 Y_{t-2} + \cdots + \phi_p Y_{t-p} + \epsilon_t\] \[Y_t = \delta + \sum_{i=1}^{p} \phi_i \cdot Y_{t-i} + \epsilon_t\] This AR model used \(p\) lags, hence we say it is of order \(p\) or \(AR(p)\).
AR(1) is then define as \[Y_t = \delta + \phi_1 Y_{t-1} + \epsilon_t\]
Few characteristics of AR models
We can simulate an AR(1) timeseries in both R and Python.
In python, we use the arima_process module from the statsmodels library.
Because these models have been developed with ARIMA in mind, we will set up the MA parameter to 1. Also, we set up the intercept to \(1\).
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.arima_process import ArmaProcess
ar1 = np.array([1, -0.9]) # the first term: the delta, the second is the phi_1
ma1 = np.array([1]) # as ma is mandatory for ArmaProcess, we set it up to 1
ar_obj1 = ArmaProcess(ar1, ma1)
sim_data1 = ar_obj1.generate_sample(nsample = 500)
plt.clf()
plt.plot(sim_data1)
plt.show()
Doing it similar with a positive \(\phi\)
ar2 = np.array([1, +0.9])
ma2 = np.array([1])
ar_obj2 = ArmaProcess(ar2, ma2)
sim_data2 = ar_obj2.generate_sample(nsample = 500)
plt.clf()
plt.plot(sim_data2)
plt.show()
Looking at the auto-correlation decay.
from statsmodels.graphics.tsaplots import plot_acf
ar3 = np.array([1, -0.5])
ma3 = np.array([1])
ar_obj3 = ArmaProcess(ar3, ma3)
sim_data3 = ar_obj3.generate_sample(nsample = 500) # to show fast decay with negative phi
plot_acf(sim_data1, alpha = 1, lags = 20)
plt.show()
plt.clf()
plot_acf(sim_data2, alpha = 1, lags = 20)
plt.show()
plt.clf()
plot_acf(sim_data3, alpha = 1, lags = 20)
plt.show()
from statsmodels.tsa.arima.model import ARIMA
model_ar = ARIMA(sim_data1, order = (1, 0, 0)) # the order ensure we are dealing with just AR model
res = model_ar.fit()
print(res.summary()) SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 500
Model: ARIMA(1, 0, 0) Log Likelihood -702.864
Date: Fri, 14 Jun 2024 AIC 1411.727
Time: 08:51:20 BIC 1424.371
Sample: 0 HQIC 1416.689
- 500
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -0.4877 0.432 -1.129 0.259 -1.334 0.359
ar.L1 0.8982 0.021 43.704 0.000 0.858 0.939
sigma2 0.9707 0.067 14.506 0.000 0.840 1.102
===================================================================================
Ljung-Box (L1) (Q): 0.28 Jarque-Bera (JB): 2.71
Prob(Q): 0.60 Prob(JB): 0.26
Heteroskedasticity (H): 1.12 Skew: -0.10
Prob(H) (two-sided): 0.46 Kurtosis: 2.69
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).print(res.param_names)['const', 'ar.L1', 'sigma2']print(res.params)[-0.48768522 0.89822033 0.97072192]Our simulated data had \(0.9\) as the parameter of the autoregressive term. The estimated parameters is quite close indeed.
We can also use the AR to make prediction.
from statsmodels.graphics.tsaplots import plot_predict
res.predict(start = 490, end = 510)array([-1.13974043, -1.50381221, -2.11834284, -1.86643043, -1.12326524,
0.25178097, 1.84163869, 2.53226982, 0.70537889, 2.57223097,
1.97822412, 1.72724467, 1.50180983, 1.29931968, 1.1174389 ,
0.95406989, 0.80732853, 0.67552245, 0.55713156, 0.45079045,
0.3552727 ])#res.plot_predict(start = 400, end = 510)
res.plot_diagnostics()
plt.show()
We could also use a specific dataset to fit an autoregressive model on.
Let’s use the famous Nile data set
import pandas as pd
import numpy as np
df_nile = pd.read_csv('../../../raw_data/Nile.csv')library(dplyr)
Attaching package: 'dplyr'The following objects are masked from 'package:stats':
filter, lagThe following objects are masked from 'package:base':
intersect, setdiff, setequal, unionlibrary(readr)
df_nile <- read_csv('../../../raw_data/Nile.csv')New names:
• `` -> `...1`Rows: 100 Columns: 3
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (3): ...1, time, Nile
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.# fit a model wit AR = 1
model_ar1 <- arima(x = df_nile$Nile, order = c(1, 0, 0))
# chek the residuals of the model (should be normallly distributed)
acf(residuals(model_ar1), main = 'Residuals of AR(1) on Nile River.')
Moving Average (MA) is another class of linear model where the outcome variable is regressed using its own previous error terms. \[Y_t = \mu + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2} + \cdots + \theta_q \epsilon_{t-q} + \epsilon_t\] This MA model used \(q\) lags, hence we say it is of order \(q\).
Putting it all together, the outcome variable of an ARIMA model can be predicted: \[Y_t = \{\delta + \phi_1 Y_{t-1} + \phi_2 Y_{t-2} + \cdots + \phi_p Y_{t-p} + \epsilon_t \} + \{\mu + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2} + \cdots + \theta_q \epsilon_{t-q} + \epsilon_t \}\] This can be simplify into: \[Y_t = \delta + \sum_{i=1}^p \phi_i Y_{t-i} + \sum_{j=1}^q \theta_j \epsilon_{t-j} + \epsilon_t\]
The parameters of an ARIMA model are (p, d, q) :
To apply an ARIMA model to a set of data, we will use the US CPI Energy component that we downloaded on the FED St-Louis website.
library(readr)
library(dplyr)
library(ggplot2)
library(modeltime)
library(timetk)
df <- read_csv('../../../raw_data/CPI_energy.csv') |>
select(date = DATE, cpi_energy = CPIENGNS)
glimpse(df)Rows: 803
Columns: 2
$ date <date> 1957-01-01, 1957-02-01, 1957-03-01, 1957-04-01, 1957-05-01…
$ cpi_energy <dbl> 21.3, 21.5, 21.6, 21.5, 21.4, 21.4, 21.5, 21.4, 21.5, 21.4,…We need first to convert our df into a ts object.
df_ts <- ts(df$cpi_energy, start = c(1957,01), frequency = 12, end = c(2023, 11))
str(df_ts) Time-Series [1:803] from 1957 to 2024: 21.3 21.5 21.6 21.5 21.4 21.4 21.5 21.4 21.5 21.4 ...ts.plot(df_ts, xlab = 'Date', ylab = 'Energy CPI')
It is usually a wise idea to check for outliers? An easy way to do this is using a boxplot.
boxplot(df_ts)
We use the ACF to determine the MA parameter (q) of the ARIMA model.
acf(df_ts, lag.max = 100)
ggacf(df_ts, num_lags = 100)
Data is clearly not stationary. We will need to use differentiation to make it stationary.
The PCAF helps determine the AR (Autoregressive) order (p) in an ARIMA model.
pacf(df_ts, lag.max = 100)
This can be confirm with Augmented Dickey Fuller test
tseries::adf.test(df_ts)Registered S3 method overwritten by 'quantmod':
method from
as.zoo.data.frame zoo
Augmented Dickey-Fuller Test
data: df_ts
Dickey-Fuller = -2.4123, Lag order = 9, p-value = 0.4038
alternative hypothesis: stationaryadf test confirm non-stationarity of our ts. We can differentiate our ts to make it stationary.
diff_ts <- diff(x = df_ts, lag = 1)
ts.plot(diff_ts)
tseries::adf.test(diff_ts)Warning in tseries::adf.test(diff_ts): p-value smaller than printed p-value
Augmented Dickey-Fuller Test
data: diff_ts
Dickey-Fuller = -9.4624, Lag order = 9, p-value = 0.01
alternative hypothesis: stationaryWe can create our training and testing set.
train_ts <- df_ts[1:793]We can now use ARIMA model using 1 and 1 for parameter (all we could see from acf)
result <- arima(train_ts, order = c(0, 1, 2))
result
Call:
arima(x = train_ts, order = c(0, 1, 2))
Coefficients:
ma1 ma2
0.5197 0.0884
s.e. 0.0356 0.0361
sigma^2 estimated as 17.24: log likelihood = -2251.54, aic = 4509.07tsdiag(result)
predict(result, 3)$pred
Time Series:
Start = 794
End = 796
Frequency = 1
[1] 290.5702 292.0037 292.0037
$se
Time Series:
Start = 794
End = 796
Frequency = 1
[1] 4.152615 7.554318 10.082648result_df <- arima(df_ts, order = c(0, 1, 2))
result_df
Call:
arima(x = df_ts, order = c(0, 1, 2))
Coefficients:
ma1 ma2
0.5033 0.0834
s.e. 0.0347 0.0358
sigma^2 estimated as 17.52: log likelihood = -2286.24, aic = 4578.49predict(result_df, 2)$pred
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
2023 273.7094
2024 273.2768
$se
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
2023 4.185297
2024 7.556805 result_df <- arima(df_ts, order = c(4, 1, 1))
result_df
Call:
arima(x = df_ts, order = c(4, 1, 1))
Coefficients:
ar1 ar2 ar3 ar4 ma1
1.1419 -0.4870 0.1896 -0.1582 -0.6576
s.e. 0.0776 0.0626 0.0531 0.0362 0.0722
sigma^2 estimated as 16.92: log likelihood = -2272.35, aic = 4556.69predict(result_df, 2)$pred
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
2023 272.8635
2024 270.8238
$se
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
2023 4.112985
2024 7.361178 forecast::auto.arima(df_ts, trace = T, stepwise = F, approximation = F)
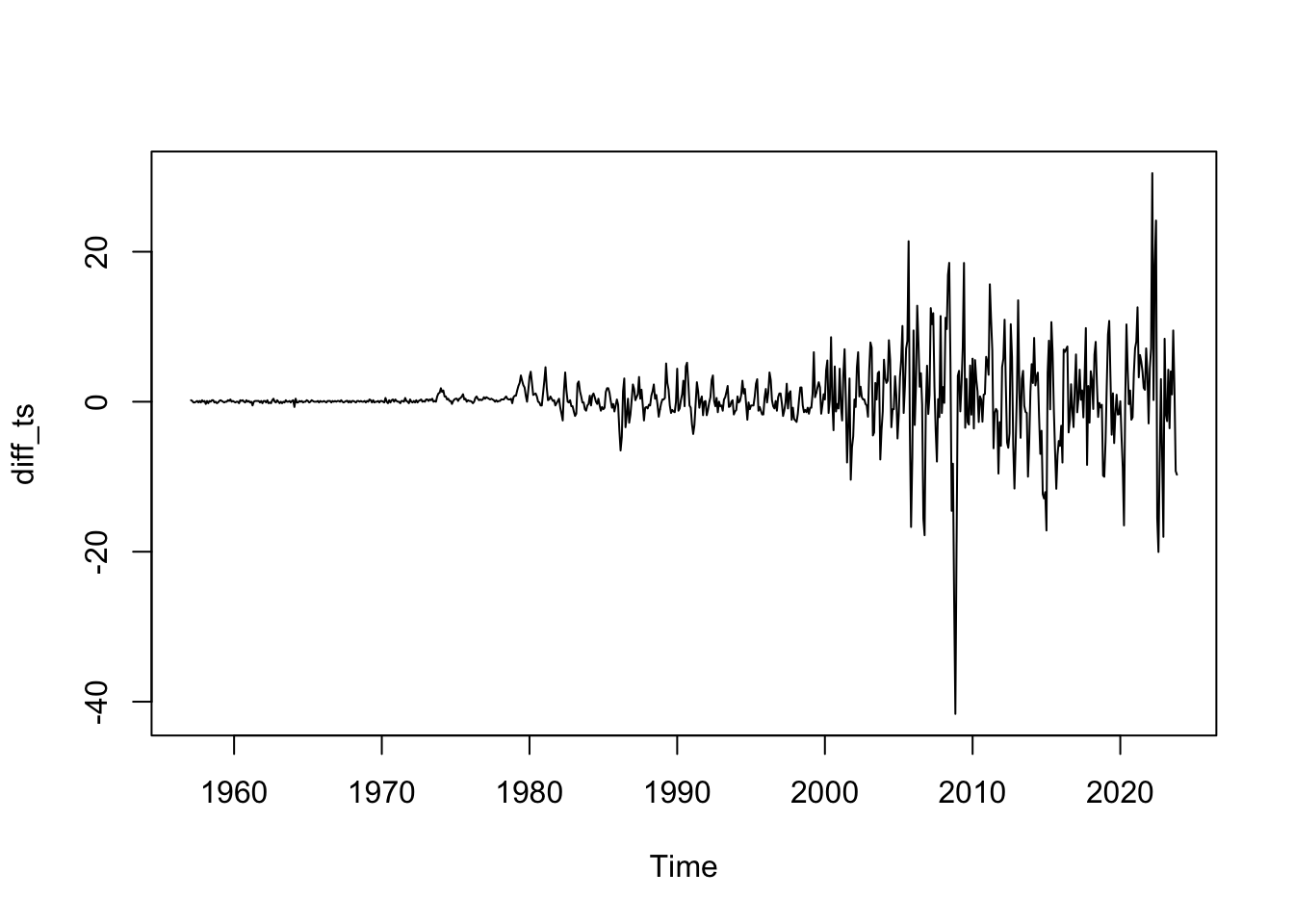
ARIMA(0,1,0) : 4762.801
ARIMA(0,1,0) with drift : 4761.123
ARIMA(0,1,0)(0,0,1)[12] : 4751.105
ARIMA(0,1,0)(0,0,1)[12] with drift : 4750.212
ARIMA(0,1,0)(0,0,2)[12] : 4749.802
ARIMA(0,1,0)(0,0,2)[12] with drift : 4749.14
ARIMA(0,1,0)(1,0,0)[12] : 4748.883
ARIMA(0,1,0)(1,0,0)[12] with drift : 4748.184
ARIMA(0,1,0)(1,0,1)[12] : Inf
ARIMA(0,1,0)(1,0,1)[12] with drift : Inf
ARIMA(0,1,0)(1,0,2)[12] : Inf
ARIMA(0,1,0)(1,0,2)[12] with drift : Inf
ARIMA(0,1,0)(2,0,0)[12] : 4742.386
ARIMA(0,1,0)(2,0,0)[12] with drift : 4742.203
ARIMA(0,1,0)(2,0,1)[12] : Inf
ARIMA(0,1,0)(2,0,1)[12] with drift : Inf
ARIMA(0,1,0)(2,0,2)[12] : Inf
ARIMA(0,1,0)(2,0,2)[12] with drift : Inf
ARIMA(0,1,1) : 4581.902
ARIMA(0,1,1) with drift : 4581.821
ARIMA(0,1,1)(0,0,1)[12] : 4577.654
ARIMA(0,1,1)(0,0,1)[12] with drift : 4577.884
ARIMA(0,1,1)(0,0,2)[12] : 4573.756
ARIMA(0,1,1)(0,0,2)[12] with drift : 4574.212
ARIMA(0,1,1)(1,0,0)[12] : 4576.446
ARIMA(0,1,1)(1,0,0)[12] with drift : 4576.758
ARIMA(0,1,1)(1,0,1)[12] : Inf
ARIMA(0,1,1)(1,0,1)[12] with drift : Inf
ARIMA(0,1,1)(1,0,2)[12] : Inf
ARIMA(0,1,1)(1,0,2)[12] with drift : Inf
ARIMA(0,1,1)(2,0,0)[12] : 4568.379
ARIMA(0,1,1)(2,0,0)[12] with drift : 4569.08
ARIMA(0,1,1)(2,0,1)[12] : Inf
ARIMA(0,1,1)(2,0,1)[12] with drift : Inf
ARIMA(0,1,1)(2,0,2)[12] : Inf
ARIMA(0,1,1)(2,0,2)[12] with drift : Inf
ARIMA(0,1,2) : 4578.515
ARIMA(0,1,2) with drift : 4578.734
ARIMA(0,1,2)(0,0,1)[12] : 4575.644
ARIMA(0,1,2)(0,0,1)[12] with drift : 4576.08
ARIMA(0,1,2)(0,0,2)[12] : 4572.671
ARIMA(0,1,2)(0,0,2)[12] with drift : 4573.279
ARIMA(0,1,2)(1,0,0)[12] : 4574.772
ARIMA(0,1,2)(1,0,0)[12] with drift : 4575.261
ARIMA(0,1,2)(1,0,1)[12] : Inf
ARIMA(0,1,2)(1,0,1)[12] with drift : Inf
ARIMA(0,1,2)(1,0,2)[12] : Inf
ARIMA(0,1,2)(1,0,2)[12] with drift : Inf
ARIMA(0,1,2)(2,0,0)[12] : 4568.289
ARIMA(0,1,2)(2,0,0)[12] with drift : 4569.079
ARIMA(0,1,2)(2,0,1)[12] : Inf
ARIMA(0,1,2)(2,0,1)[12] with drift : Inf
ARIMA(0,1,3) : 4579.677
ARIMA(0,1,3) with drift : 4580.023
ARIMA(0,1,3)(0,0,1)[12] : 4577.191
ARIMA(0,1,3)(0,0,1)[12] with drift : 4577.708
ARIMA(0,1,3)(0,0,2)[12] : 4574.269
ARIMA(0,1,3)(0,0,2)[12] with drift : 4574.946
ARIMA(0,1,3)(1,0,0)[12] : 4576.379
ARIMA(0,1,3)(1,0,0)[12] with drift : 4576.941
ARIMA(0,1,3)(1,0,1)[12] : Inf
ARIMA(0,1,3)(1,0,1)[12] with drift : Inf
ARIMA(0,1,3)(2,0,0)[12] : 4569.998
ARIMA(0,1,3)(2,0,0)[12] with drift : 4570.839
ARIMA(0,1,4) : 4581.69
ARIMA(0,1,4) with drift : 4582.053
ARIMA(0,1,4)(0,0,1)[12] : 4579.221
ARIMA(0,1,4)(0,0,1)[12] with drift : 4579.733
ARIMA(0,1,4)(1,0,0)[12] : 4578.408
ARIMA(0,1,4)(1,0,0)[12] with drift : 4578.96
ARIMA(0,1,5) : 4583.72
ARIMA(0,1,5) with drift : 4584.063
ARIMA(1,1,0) : 4592.114
ARIMA(1,1,0) with drift : 4592.78
ARIMA(1,1,0)(0,0,1)[12] : 4590.795
ARIMA(1,1,0)(0,0,1)[12] with drift : 4591.591
ARIMA(1,1,0)(0,0,2)[12] : 4589.897
ARIMA(1,1,0)(0,0,2)[12] with drift : 4590.8
ARIMA(1,1,0)(1,0,0)[12] : 4590.336
ARIMA(1,1,0)(1,0,0)[12] with drift : 4591.158
ARIMA(1,1,0)(1,0,1)[12] : Inf
ARIMA(1,1,0)(1,0,1)[12] with drift : Inf
ARIMA(1,1,0)(1,0,2)[12] : Inf
ARIMA(1,1,0)(1,0,2)[12] with drift : Inf
ARIMA(1,1,0)(2,0,0)[12] : 4587.308
ARIMA(1,1,0)(2,0,0)[12] with drift : 4588.314
ARIMA(1,1,0)(2,0,1)[12] : Inf
ARIMA(1,1,0)(2,0,1)[12] with drift : Inf
ARIMA(1,1,0)(2,0,2)[12] : Inf
ARIMA(1,1,0)(2,0,2)[12] with drift : Inf
ARIMA(1,1,1) : 4577.984
ARIMA(1,1,1) with drift : 4578.289
ARIMA(1,1,1)(0,0,1)[12] : 4575.351
ARIMA(1,1,1)(0,0,1)[12] with drift : 4575.838
ARIMA(1,1,1)(0,0,2)[12] : 4572.434
ARIMA(1,1,1)(0,0,2)[12] with drift : 4573.078
ARIMA(1,1,1)(1,0,0)[12] : 4574.518
ARIMA(1,1,1)(1,0,0)[12] with drift : 4575.051
ARIMA(1,1,1)(1,0,1)[12] : Inf
ARIMA(1,1,1)(1,0,1)[12] with drift : Inf
ARIMA(1,1,1)(1,0,2)[12] : Inf
ARIMA(1,1,1)(1,0,2)[12] with drift : Inf
ARIMA(1,1,1)(2,0,0)[12] : 4568.139
ARIMA(1,1,1)(2,0,0)[12] with drift : 4568.95
ARIMA(1,1,1)(2,0,1)[12] : Inf
ARIMA(1,1,1)(2,0,1)[12] with drift : Inf
ARIMA(1,1,2) : 4579.966
ARIMA(1,1,2) with drift : 4580.292
ARIMA(1,1,2)(0,0,1)[12] : 4577.355
ARIMA(1,1,2)(0,0,1)[12] with drift : 4577.857
ARIMA(1,1,2)(0,0,2)[12] : 4574.418
ARIMA(1,1,2)(0,0,2)[12] with drift : 4575.085
ARIMA(1,1,2)(1,0,0)[12] : 4576.524
ARIMA(1,1,2)(1,0,0)[12] with drift : 4577.071
ARIMA(1,1,2)(1,0,1)[12] : Inf
ARIMA(1,1,2)(1,0,1)[12] with drift : Inf
ARIMA(1,1,2)(2,0,0)[12] : 4570.12
ARIMA(1,1,2)(2,0,0)[12] with drift : 4570.951
ARIMA(1,1,3) : 4581.695
ARIMA(1,1,3) with drift : 4582.053
ARIMA(1,1,3)(0,0,1)[12] : 4579.222
ARIMA(1,1,3)(0,0,1)[12] with drift : 4579.743
ARIMA(1,1,3)(1,0,0)[12] : 4578.411
ARIMA(1,1,3)(1,0,0)[12] with drift : 4578.979
ARIMA(1,1,4) : 4573.756
ARIMA(1,1,4) with drift : 4571.09
ARIMA(2,1,0) : 4579.505
ARIMA(2,1,0) with drift : 4579.69
ARIMA(2,1,0)(0,0,1)[12] : 4577.142
ARIMA(2,1,0)(0,0,1)[12] with drift : 4577.505
ARIMA(2,1,0)(0,0,2)[12] : 4575.062
ARIMA(2,1,0)(0,0,2)[12] with drift : 4575.574
ARIMA(2,1,0)(1,0,0)[12] : 4576.421
ARIMA(2,1,0)(1,0,0)[12] with drift : 4576.826
ARIMA(2,1,0)(1,0,1)[12] : Inf
ARIMA(2,1,0)(1,0,1)[12] with drift : Inf
ARIMA(2,1,0)(1,0,2)[12] : Inf
ARIMA(2,1,0)(1,0,2)[12] with drift : Inf
ARIMA(2,1,0)(2,0,0)[12] : 4571.428
ARIMA(2,1,0)(2,0,0)[12] with drift : 4572.095
ARIMA(2,1,0)(2,0,1)[12] : Inf
ARIMA(2,1,0)(2,0,1)[12] with drift : Inf
ARIMA(2,1,1) : 4579.893
ARIMA(2,1,1) with drift : 4580.248
ARIMA(2,1,1)(0,0,1)[12] : 4577.321
ARIMA(2,1,1)(0,0,1)[12] with drift : 4577.839
ARIMA(2,1,1)(0,0,2)[12] : 4574.356
ARIMA(2,1,1)(0,0,2)[12] with drift : 4575.04
ARIMA(2,1,1)(1,0,0)[12] : 4576.493
ARIMA(2,1,1)(1,0,0)[12] with drift : 4577.055
ARIMA(2,1,1)(1,0,1)[12] : Inf
ARIMA(2,1,1)(1,0,1)[12] with drift : Inf
ARIMA(2,1,1)(2,0,0)[12] : 4570.052
ARIMA(2,1,1)(2,0,0)[12] with drift : 4570.9
ARIMA(2,1,2) : 4581.576
ARIMA(2,1,2) with drift : 4582.003
ARIMA(2,1,2)(0,0,1)[12] : Inf
ARIMA(2,1,2)(0,0,1)[12] with drift : Inf
ARIMA(2,1,2)(1,0,0)[12] : Inf
ARIMA(2,1,2)(1,0,0)[12] with drift : Inf
ARIMA(2,1,3) : Inf
ARIMA(2,1,3) with drift : Inf
ARIMA(3,1,0) : 4581.026
ARIMA(3,1,0) with drift : 4581.307
ARIMA(3,1,0)(0,0,1)[12] : 4578.438
ARIMA(3,1,0)(0,0,1)[12] with drift : 4578.91
ARIMA(3,1,0)(0,0,2)[12] : 4575.713
ARIMA(3,1,0)(0,0,2)[12] with drift : 4576.374
ARIMA(3,1,0)(1,0,0)[12] : 4577.627
ARIMA(3,1,0)(1,0,0)[12] with drift : 4578.148
ARIMA(3,1,0)(1,0,1)[12] : Inf
ARIMA(3,1,0)(1,0,1)[12] with drift : Inf
ARIMA(3,1,0)(2,0,0)[12] : 4571.48
ARIMA(3,1,0)(2,0,0)[12] with drift : 4572.324
ARIMA(3,1,1) : 4581.285
ARIMA(3,1,1) with drift : 4581.576
ARIMA(3,1,1)(0,0,1)[12] : 4578.762
ARIMA(3,1,1)(0,0,1)[12] with drift : 4579.224
ARIMA(3,1,1)(1,0,0)[12] : 4577.945
ARIMA(3,1,1)(1,0,0)[12] with drift : 4578.452
ARIMA(3,1,2) : 4568.698
ARIMA(3,1,2) with drift : Inf
ARIMA(4,1,0) : 4575.634
ARIMA(4,1,0) with drift : 4575.534
ARIMA(4,1,0)(0,0,1)[12] : 4574.175
ARIMA(4,1,0)(0,0,1)[12] with drift : 4574.312
ARIMA(4,1,0)(1,0,0)[12] : 4573.622
ARIMA(4,1,0)(1,0,0)[12] with drift : 4573.812
ARIMA(4,1,1) : 4556.801
ARIMA(4,1,1) with drift : 4554.628
ARIMA(5,1,0) : 4561.352
ARIMA(5,1,0) with drift : 4560.508
Best model: ARIMA(4,1,1) with drift Series: df_ts
ARIMA(4,1,1) with drift
Coefficients:
ar1 ar2 ar3 ar4 ma1 drift
1.1535 -0.4942 0.1912 -0.1603 -0.6749 0.3205
s.e. 0.0758 0.0622 0.0534 0.0365 0.0703 0.1523
sigma^2 = 16.95: log likelihood = -2270.24
AIC=4554.49 AICc=4554.63 BIC=4587.3df |> plot_time_series(date, cpi_energy, .interactive = FALSE)
with model time, it is pretty easy to do get the value for arima.
cv_splits <- df |>
time_series_split(date_var = date, assess = '13 months', cumulative = TRUE)
cv_splits |>
tk_time_series_cv_plan() |>
plot_time_series_cv_plan(.date_var = date, .value = cpi_energy, .interactive = FALSE)
library(tidymodels)── Attaching packages ────────────────────────────────────── tidymodels 1.2.0 ──✔ broom 1.0.6 ✔ rsample 1.2.1
✔ dials 1.2.1 ✔ tibble 3.2.1
✔ infer 1.0.7 ✔ tidyr 1.3.1
✔ modeldata 1.3.0 ✔ tune 1.2.1
✔ parsnip 1.2.1 ✔ workflows 1.1.4
✔ purrr 1.0.2 ✔ workflowsets 1.1.0
✔ recipes 1.0.10 ✔ yardstick 1.3.1 Warning: package 'broom' was built under R version 4.3.3── Conflicts ───────────────────────────────────────── tidymodels_conflicts() ──
✖ purrr::discard() masks scales::discard()
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
✖ yardstick::spec() masks readr::spec()
✖ recipes::step() masks stats::step()
• Dig deeper into tidy modeling with R at https://www.tmwr.orglibrary(parsnip)
library(modeltime)
model_fit_arima <- arima_reg() |>
set_engine('auto_arima') |>
fit(cpi_energy ~ date, training(cv_splits))frequency = 12 observations per 1 yearmodel_fit_arimaparsnip model object
Series: outcome
ARIMA(0,1,2)(0,0,2)[12]
Coefficients:
ma1 ma2 sma1 sma2
0.5229 0.0895 0.0733 0.0907
s.e. 0.0356 0.0358 0.0400 0.0359
sigma^2 = 16.45: log likelihood = -2222.54
AIC=4455.07 AICc=4455.15 BIC=4478.42