This post is about how to use Kmeans to classify various market regimes or to use Kmeans to classify financial observations.

Market regime

Financial markets have the tendency to change their behavior over time, which can create regimes, or periods of fairly persistent market conditions. Investors often look to discern the current market regime, looking out for any changes to it and how those might affect the individual components of their portfolio asset allocation. Modeling various market regimes can be an effective tool, as it can enable macro-economically aware investment decision-making and better management of tail risks.

With K-means we are trying to establish groups of data that are homegenous and distinctly different from other groups. The K- stands for the number of clusters we will create.

The concept of distance comes in when deciding if a data point belongs to a cluster. The most common way to measure distance is the Euclidean Distance.

With multivariate data set, it is important to normalize the data.
A usual rule of thumb is to set the number of clusters as the square root of the number of observation.

Using R

Load up packages and read data

library(readr)        # load and read .csv file
library(glue)         # concatenate strings together
library(dplyr)        # the tidy plyr tool for data wrangling
library(tidyr)        # to use the drop_na function
the_path <- here::here()
df <- read_csv(glue(the_path, "/raw_data/AMD.csv")) |> 
  rename(adj_close = 'adjClose') |> 
  select(date, high, low, close, adj_close)
glimpse(df)

Rows: 5,822
Columns: 5
$ date      <date> 2024-02-23, 2024-02-22, 2024-02-21, 2024-02-20, 2024-02-16,…
$ high      <dbl> 183.8000, 183.8300, 164.9000, 171.8100, 180.3301, 180.5000, …
$ low       <dbl> 176.9500, 172.0000, 161.8100, 162.0000, 173.2500, 175.2600, …
$ close     <dbl> 177.53, 181.86, 164.29, 165.69, 173.87, 176.76, 178.70, 171.…
$ adj_close <dbl> 177.53, 181.86, 164.29, 165.69, 173.87, 176.76, 178.70, 171.…

Feature engineering

library(TTR)      # The technical analysis package
yo <- aroon(df[, c('high', 'low')], n = 23)
df$aroon <- yo[, 3]
yo <- CCI(df[, c('high', 'low', 'close')], n = 17)
df$cci <- yo
yo <- chaikinVolatility(df[, c('high', 'low')], n = 13)
df$chaikinVol <- yo
df1 <- df |> 
  select(date, aroon, cci, chaikinVol, adj_close) |> 
  mutate(across(c(aroon, cci, chaikinVol), ~ as.numeric(scale(.)))) |>
  drop_na()
skimr::skim(df1 %>% select(-date))

Data summary
Name	df1 %>% select(-date)
Number of rows	5797
Number of columns	4
_______________________
Column type frequency:
numeric	4
________________________
Group variables	None

Variable type: numeric

skim_variable	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
aroon	1	0.00	1.00	-1.49	-0.94	-0.19	0.90	1.65	▇▆▂▆▆
cci	1	0.00	1.00	-4.66	-0.78	-0.08	0.80	4.07	▁▂▇▅▁
chaikinVol	1	0.00	1.00	-2.49	-0.70	-0.11	0.59	4.40	▂▇▅▁▁
adj_close	1	25.52	32.97	1.62	5.70	12.14	26.00	162.67	▇▁▁▁▁

# also good to check for correlation between variables. 
library(corrr)
df1 |> select(-date, -adj_close) |> 
  correlate() |> 
  rearrange() |> 
  shave()

# A tibble: 3 × 4
  term          cci  aroon chaikinVol
  <chr>       <dbl>  <dbl>      <dbl>
1 cci        NA     NA             NA
2 aroon       0.564 NA             NA
3 chaikinVol  0.209  0.227         NA

These 3 variables seem to complete each other well as little to-no correlation.

Create clusters

library(purrr)     #use the map function
library(broom)     #use the glance function on kmeans 
df1sc <- df1 %>% select(-date, -adj_close)
kclusts <- tibble(k = 1:9) |> 
  mutate(kclust = map(k, ~kmeans(df1sc, centers = .x, nstart = 30, iter.max = 50L)), 
         glanced = map(kclust, glance), 
         augmented = map(kclust, augment, df1))
kclusts |> unnest(cols = c('glanced'))

# A tibble: 9 × 7
      k kclust    totss tot.withinss betweenss  iter augmented           
  <int> <list>    <dbl>        <dbl>     <dbl> <int> <list>              
1     1 <kmeans> 17389.       17389. -6.55e-11     1 <tibble [5,797 × 6]>
2     2 <kmeans> 17389.       10193.  7.20e+ 3     1 <tibble [5,797 × 6]>
3     3 <kmeans> 17389.        8212.  9.18e+ 3     4 <tibble [5,797 × 6]>
4     4 <kmeans> 17389.        6658.  1.07e+ 4     4 <tibble [5,797 × 6]>
5     5 <kmeans> 17389.        5684.  1.17e+ 4     4 <tibble [5,797 × 6]>
6     6 <kmeans> 17389.        4790.  1.26e+ 4     5 <tibble [5,797 × 6]>
7     7 <kmeans> 17389.        4349.  1.30e+ 4     4 <tibble [5,797 × 6]>
8     8 <kmeans> 17389.        3922.  1.35e+ 4     5 <tibble [5,797 × 6]>
9     9 <kmeans> 17389.        3600.  1.38e+ 4     5 <tibble [5,797 × 6]>

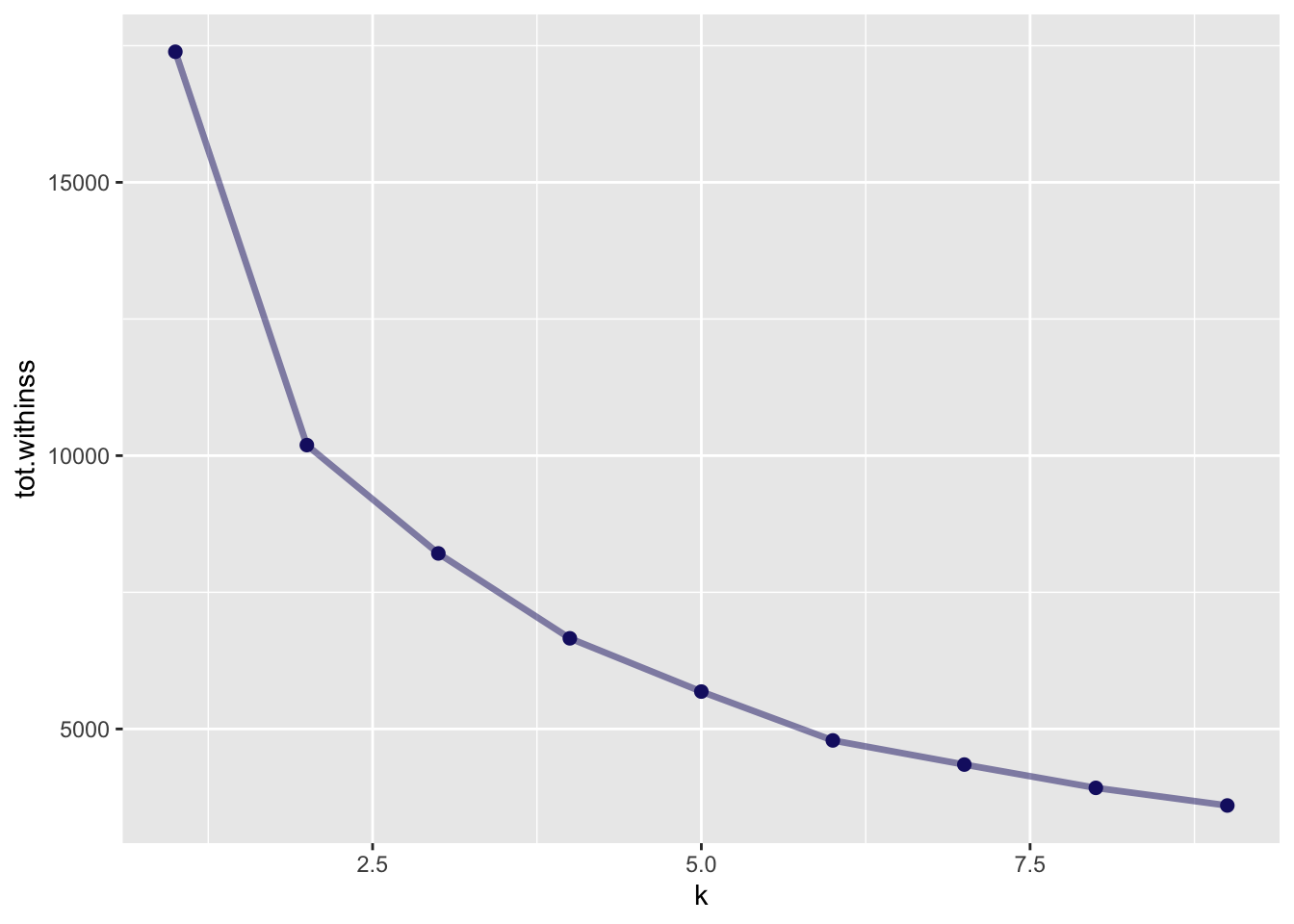
There are several ways to choose the ideal number of clusters. One of them is the elbow method, another one is the Silhouette Method.

The tot.withinss is the total within-cluster sum of square. This is the value used for the eblow method.

For the Silhouette Method, we can use the cluster package.

avg_sil <- function(k) { 
  kmeans_object <- kmeans(df1sc, centers = k, iter.max = 50L)
  silh = cluster::silhouette(kmeans_object$cluster, dist(df1sc))
  mean(silh[, 3])
  }
# Compute and plot wss for k = 2 to k = 15
yo <- tibble(k_values =  2:9) |> 
  mutate(avg_sil_values = map_dbl(k_values, avg_sil))
yo

# A tibble: 8 × 2
  k_values avg_sil_values
     <int>          <dbl>
1        2          0.376
2        3          0.315
3        4          0.285
4        5          0.302
5        6          0.313
6        7          0.309
7        8          0.287
8        9          0.288

A more elegant way to do that, using this post from SO

yo <- kclusts |> 
  mutate(silhouetted = map(augmented, ~ cluster::silhouette(as.numeric(levels(.x$.cluster))[.x$.cluster], dist(df1sc)))) |> 
  select(k, silhouetted) |> unnest(cols=c('silhouetted')) |> 
  group_by(k) %>% 
  summarise(avg_sil_values = mean(silhouetted[,3]))
yo

# A tibble: 9 × 2
      k avg_sil_values
  <int>          <dbl>
1     1         NA    
2     2          0.376
3     3          0.315
4     4          0.285
5     5          0.302
6     6          0.313
7     7          0.291
8     8          0.287
9     9          0.285

Some visualizations

Elbow method

library(ggplot2)
kclusts |> 
  unnest(cols = c('glanced')) |> 
  ggplot(aes(k, tot.withinss)) + 
  geom_line(alpha = 0.5, size = 1.2, color = 'midnightblue') + 
  geom_point(size = 2, color = 'midnightblue')

Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.

Total within-cluster sum of square for k-cluster

Based on the elbow method, I would be tempted to choose to 5 clusters (2 seems another obvious one).

Silhouette Method

yo |> ggplot(aes(k, avg_sil_values)) + 
  geom_line(alpha = 0.5, size = 1.2, color = 'midnightblue') + 
  geom_point(size = 2, color = 'midnightblue')

Warning: Removed 1 row containing missing values or values outside the scale range
(`geom_line()`).

Warning: Removed 1 row containing missing values or values outside the scale range
(`geom_point()`).

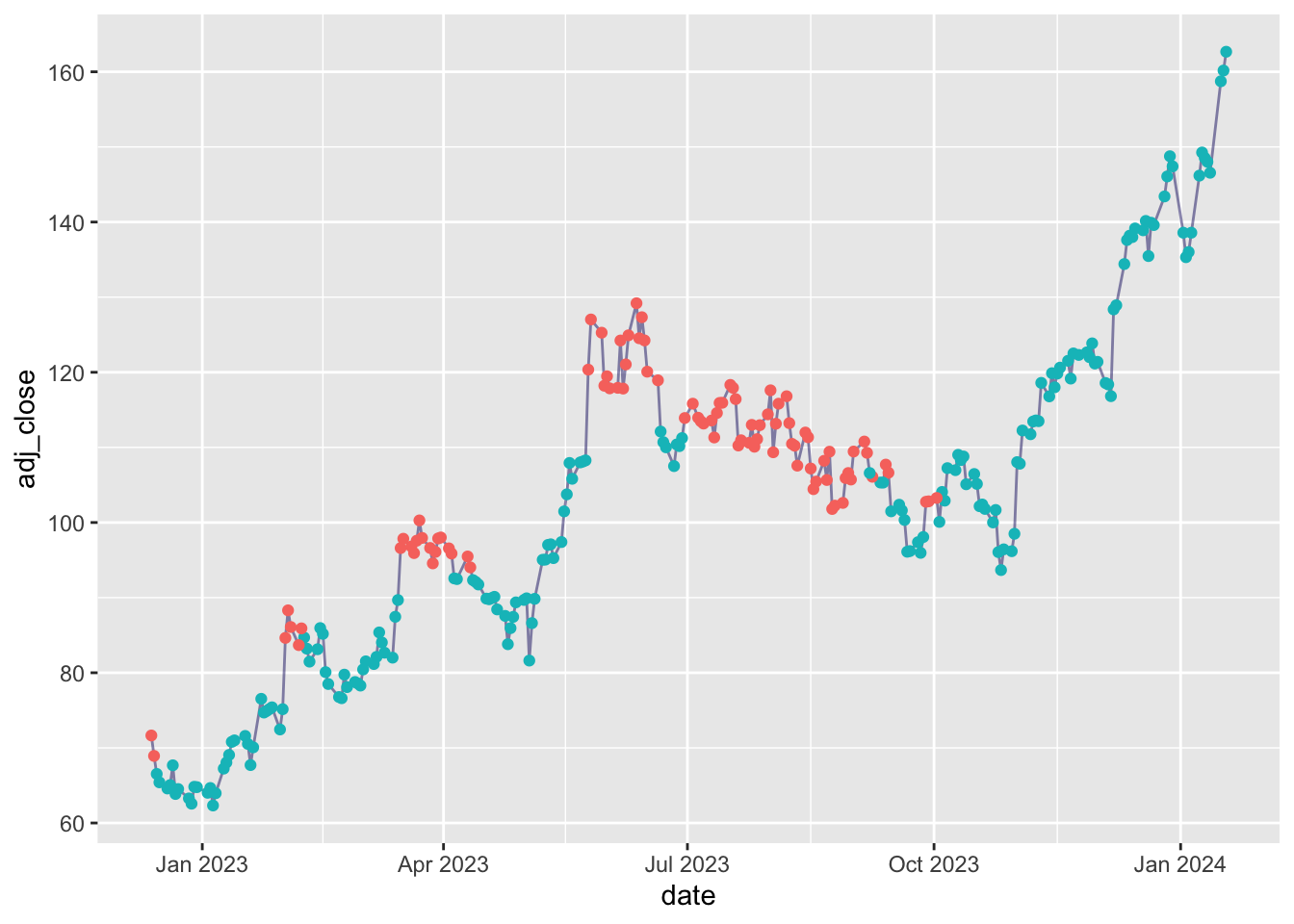
2 is the winner ;-)

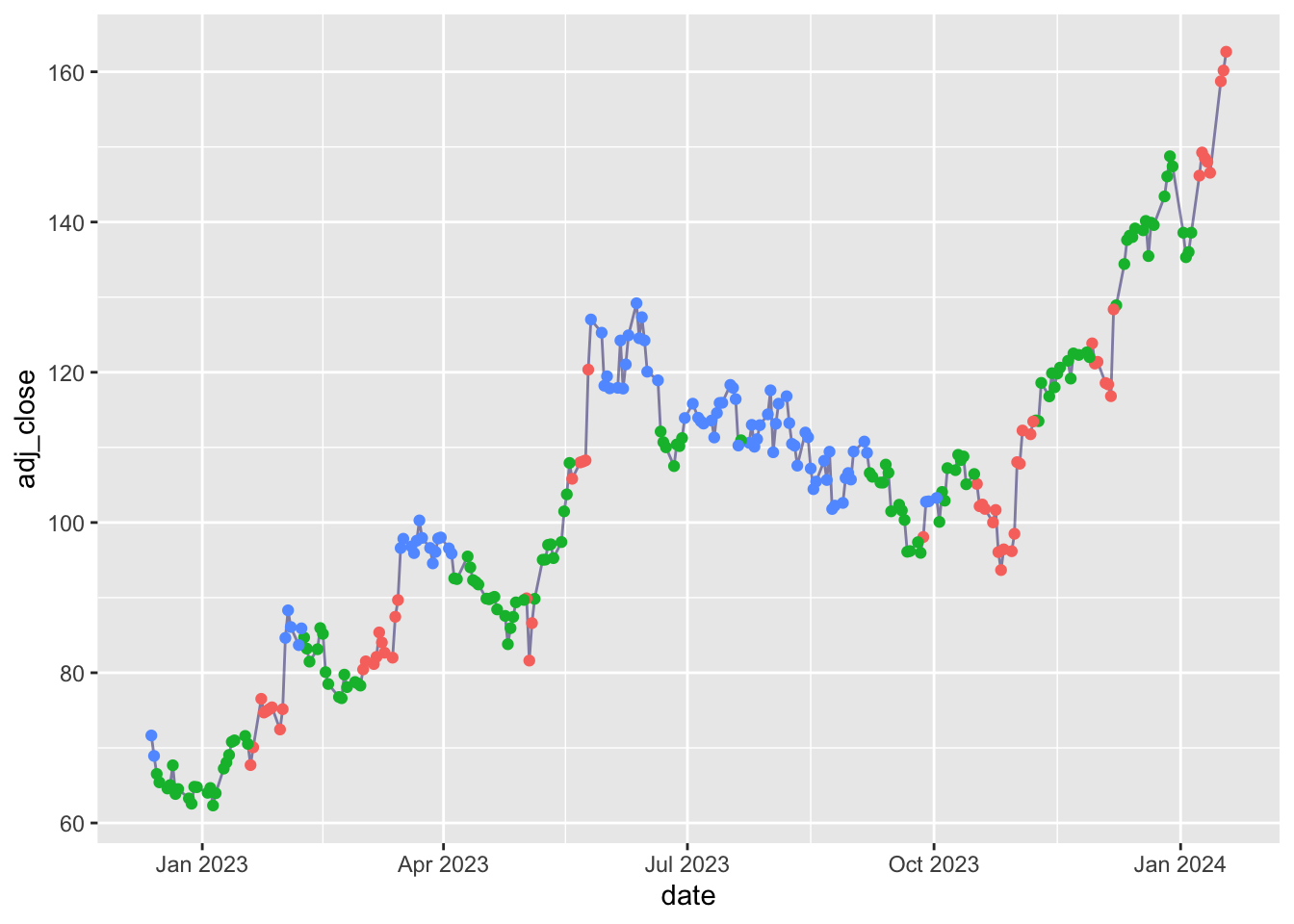
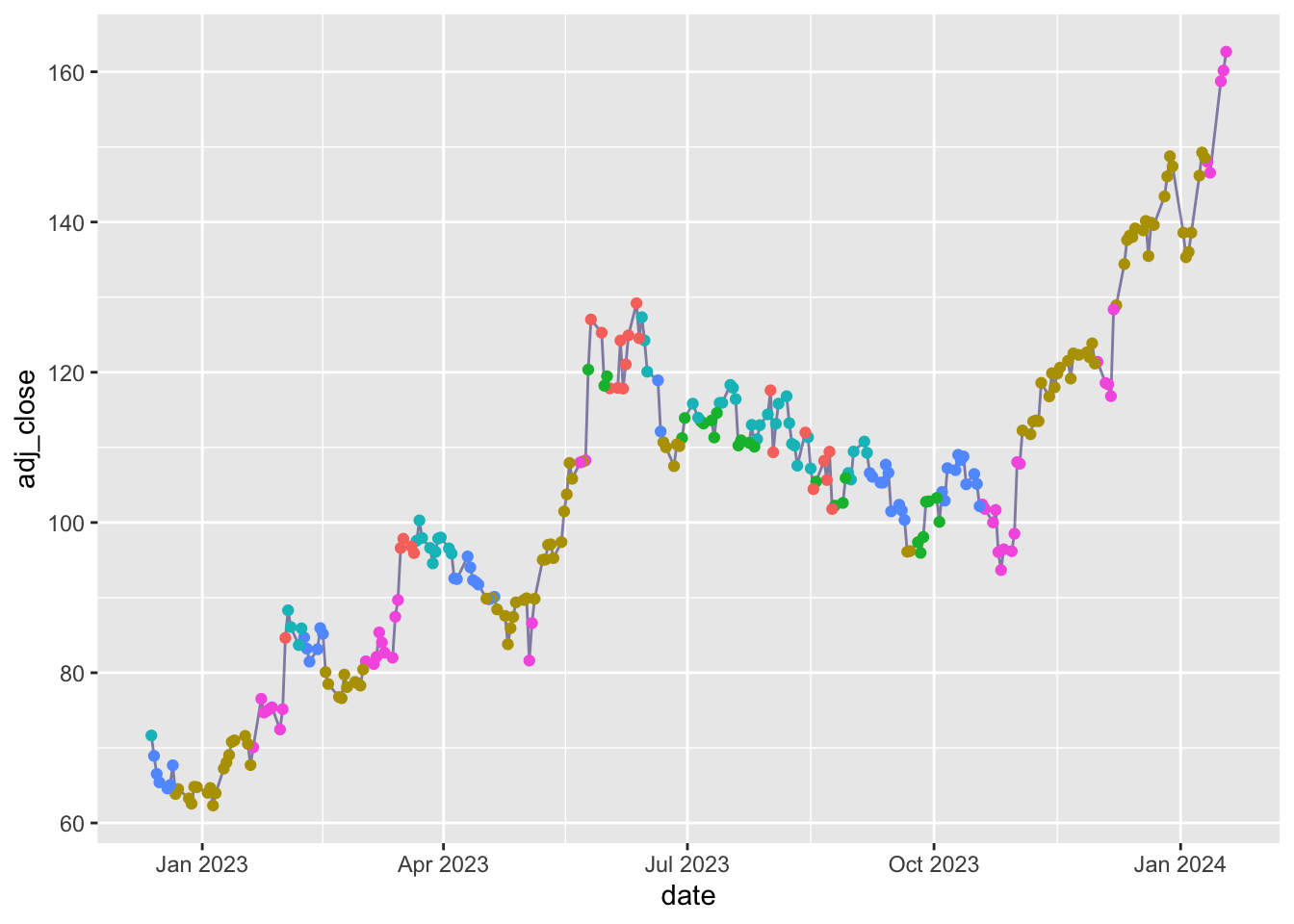
Plotting the stocks with clustered observations

library(lubridate)
yo <- kmeans(df1 |> select(-date, -adj_close), centers = 2)
augment(yo, df1) |> filter(date >= today() - 500) |> 
  ggplot(aes(x = date, y = adj_close)) + 
    geom_line(alpha = 0.5, color = 'midnightblue') + 
    geom_point(aes(color = .cluster)) + 
    theme(legend.position = 'none')

Plotting adjusted close price with only 2 clusters

yo <- kmeans(df1 |> select(-date, -adj_close), centers = 3)
augment(yo, df1) |> filter(date >= today() - 500) |> 
  ggplot(aes(x = date, y = adj_close)) + 
    geom_line(alpha = 0.5, color = 'midnightblue') + 
    geom_point(aes(color = .cluster)) + 
    theme(legend.position = 'none')

Plotting adjusted close price with only 3 clusters

yo <- kmeans(df1 |> select(-date, -adj_close), centers = 6)
augment(yo, df1) |> filter(date >= today() - 500) |> 
  ggplot(aes(x = date, y = adj_close)) + 
    geom_line(alpha = 0.5, color = 'midnightblue') + 
    geom_point(aes(color = .cluster)) + 
    theme(legend.position = 'none')

Plotting adjusted close price with only 6 clusters

Using python

Original blog post

import yfinance as yf     #only to download data
data  = yf.download("AMD")
data.to_csv("../../raw_data/AMD.csv")

import pandas as pd
py_df = pd.read_csv("../../raw_data/intc.csv", names = ['date', 'open', 'high', 'low', 'close', 'adj_close', 'volume']).iloc[1: , :]
py_df.tail()
py_df.info()
py_df.shape
py_df_melt = py_df.melt(id_vars = 'date', value_vars = ['open', 'high', 'low', 'close'], value_name = 'prices', var_name = 'price_point')
py_df_melt.info()
py_df_melt.shape

Let’s graph the last year of data

import matplotlib.pyplot as plt
ta_df2 = ta_df.tail(250).copy()
ta_df2['adj_close'] = py_df['adj_close']
ta_df2['date_time'] = pd.to_datetime(ta_df2['date_time'], utc=True)
ta_df2['adj_close'] = pd.to_numeric(ta_df2['adj_close'])
fig = plt.figure(figsize = (12, 8)) 
gs = fig.add_gridspec(3, hspace=0)
axs = gs.subplots(sharex=True)
#plt.figure(figsize = (12, 8))
axs[0].plot(ta_df2['date_time'], ta_df2['adj_close'])
axs[0].set_ylim(25, 55)
#axs[0].set_title('INTC price')
axs[1].plot(ta_df2['date_time'], ta_df2['aaron'],  'tab:green')
axs[1].set_ylim(-105, 105)
#axs[1].set_title('Aaron ind.')
axs[2].plot(ta_df2['date_time'], ta_df2['ht'], 'tab:red')
axs[2].set_ylim(-50,320)
for ax in axs:
    ax.label_outer()
    
plt.show()

from sklearn.metrics import silhouette_score
from sklearn.cluster import KMeans
inertia = []
sil_score = []
ta_df.pop('date_time')
for n_clusters in range(2, 14): 
  kmeans = KMeans(n_clusters = n_clusters, random_state=0)
  preds = kmeans.fit_predict(ta_df)
  inertia.append(kmeans.inertia_ / n_clusters)
  sil_score.append(silhouette_score(ta_df, preds))
  
inertias = pd.DataFrame({n_clusters: range(2, 14), "inertia": inertia})
sil_scores = pd.DataFrame({n_clusters: range(2, 14), "sil_score": sil_score})
print(inertias)
print(sil_scores)