x = [4, 5, 10, 4, 3, 11, 14 , 8, 10, 12]
y = [21, 19, 24, 17, 16, 25, 24, 22, 21, 21]
classes = [0, 0, 1, 0, 0, 1, 1, 0, 1, 1]
import matplotlib.pyplot as plt
plt.scatter(x, y, c = classes)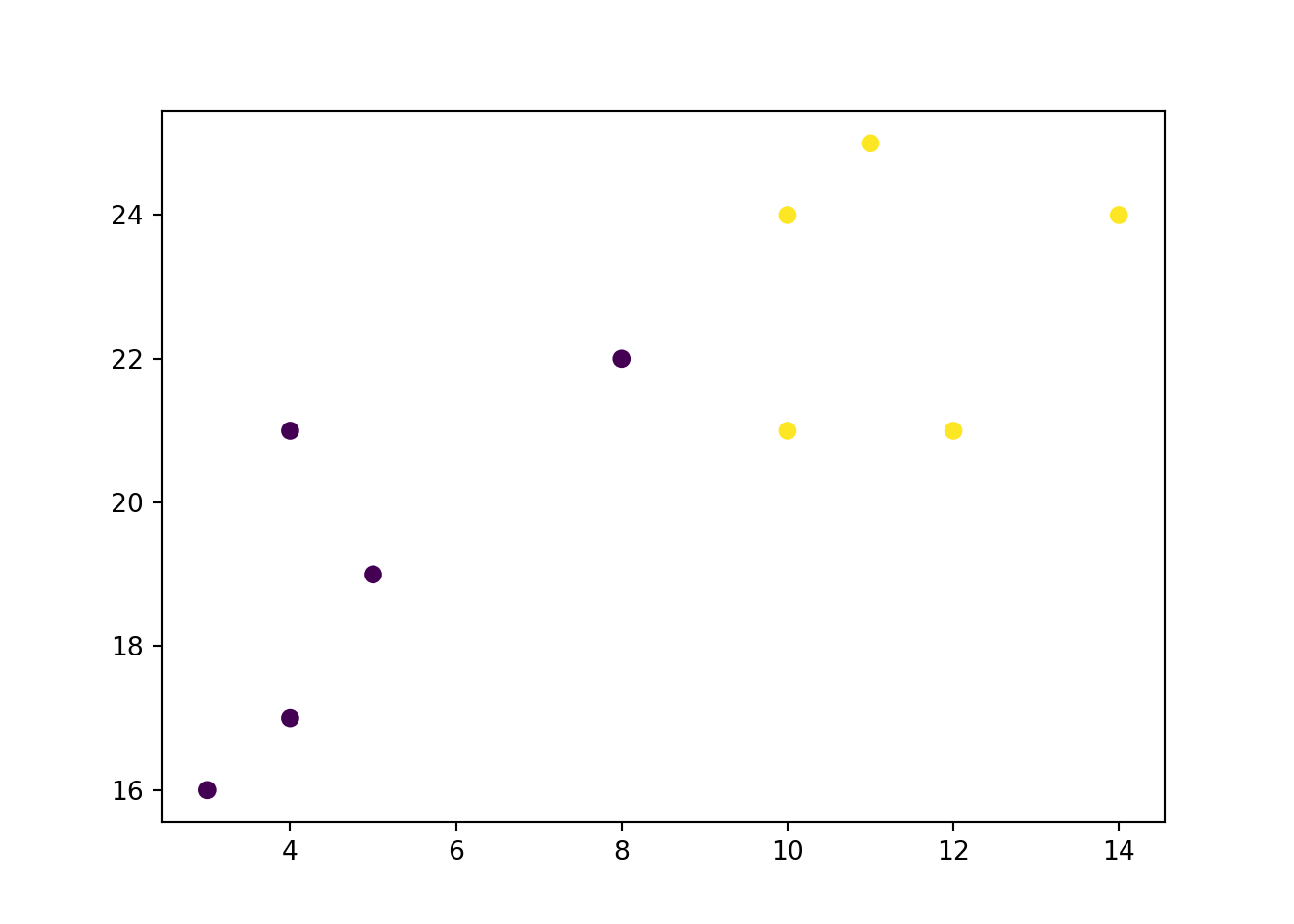
François de Ryckel
November 14, 2023
April 21, 2024
One of the very first ML algorithm (because of its ease) I expose is KNN. In this post, we’ll learn about KNN using Python (with the Sklearn package) and using R with packages from the tidymodel framework.
KNN stands for K Nearest Neighbor.
KNN is not really a machine learning techniques in the sense that it trains a model. In the case of KNN, there is no training. We are waiting for test data to see what label (or value) will the the new data will get. We then say that KNN is a lazy learner (as opposed to eager learners like SVM or RF). Nonetheless, it is a supervised ML algorithm that can be used for both classification and regression. The intuition behind the model is that observations that are closed to each other (close in terms of distance in a hyperplane) have similar labels (classification) or values (regression).
As mentioned, there is no training phase when using KNN. Instead, there is only prediction.
We take an observation and check the K observations next to it. We check the label of the K observations next to our data to be labeled and using a majority voting system we assign the label. For regression, it calculates the average or weighted average of the target values of the K neighbors to predict the value for the input data point.

Looking at the above image, we can see that, using k=3, the 3 observations closest to the star (our data to be classified) are all brown circle. Hence we should classify the star as a brown circle instead of an orange rectangle.
Because KNN use distance, it is important to scale the data as a pre-processing steps. Otherwise, features with big scale (let’s say price) will skew the distance against features with lower scale (let’s say percentage).
Using probability terminology, one can say that KNN method is a direct attempt at approximating the conditional expectation using actual data.
In the case of regression, the estimation function could be written as \[\hat{f}(x) = \text{Average } [y_i|x_i \in \mathcal{N}_k(x)]\] where \(\mathcal{N}_k (x)\) is the neighborhood of x containing the k-closest observations.
In the case of classification, we use a majority voting system.
x = [4, 5, 10, 4, 3, 11, 14 , 8, 10, 12]
y = [21, 19, 24, 17, 16, 25, 24, 22, 21, 21]
classes = [0, 0, 1, 0, 0, 1, 1, 0, 1, 1]
import matplotlib.pyplot as plt
plt.scatter(x, y, c = classes)
Now let’s create a KNN object and a new point
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors = 3)
knn.fit(list(zip(x, y)), classes)KNeighborsClassifier(n_neighbors=3)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
KNeighborsClassifier(n_neighbors=3)
new_x = 3
new_y = 20
new_point = [(new_x, new_y)]
prediction = knn.predict(new_point)
plt.scatter(x + [new_x], y + [new_y], c = classes + [prediction[0]])
plt.text(x = new_x-1, y = new_y-1, s = f"new point, class:{prediction[0]}")
library(dplyr)
library(ggplot2)
df <- tibble(x = c(4, 5, 10, 4, 3, 11, 14 , 8, 10, 12),
y = c(21, 19, 24, 17, 16, 25, 24, 22, 21, 21),
classes = as.factor(c(0, 0, 1, 0, 0, 1, 1, 0, 1, 1)))
ggplot(df, aes(x = x, y = y, color = classes)) +
geom_point() +
theme(legend.position = 'none')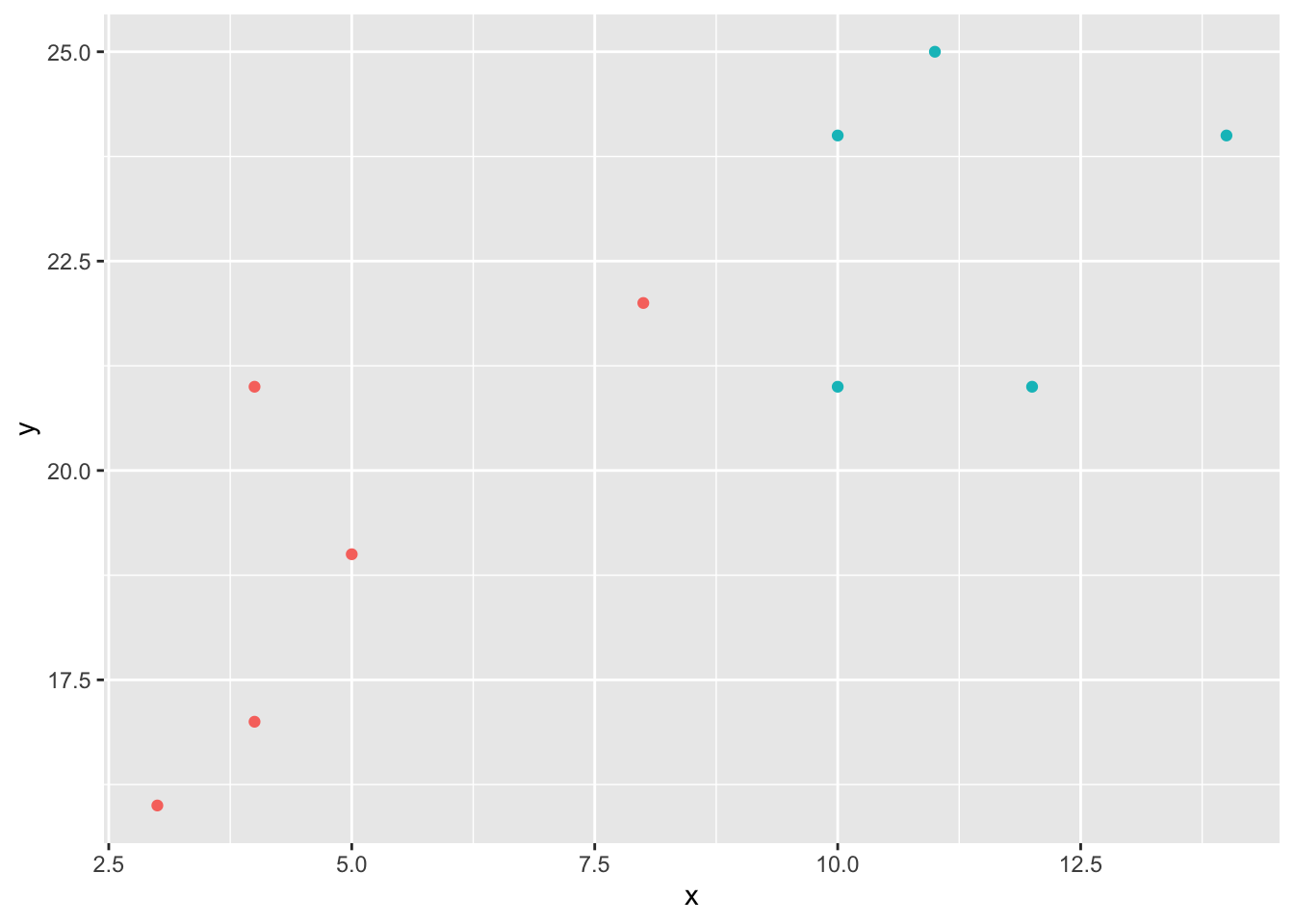
Using the tidymodel framework, we are first creating a recipe. In the tidymodel framework, a recipe apply transformations to the original data set. In our case the only needed transformation is scaling. Next, we apply that scaling transformation to the new point.
Using ‘parnsip’, we create the KNN object.
library(recipes)
library(parsnip)
# create a recipe
df_rec <- recipe(classes ~ ., data = df) |>
step_scale(-classes) |>
prep()
# apply the recipe on our dataset (using 'juice()')
df_juiced <- juice(df_rec)
new_point = tibble(x = c(3), y = c(20))
# apply the recipe on new data (using 'bake()')
df_baked <- bake(df_rec, new_data = new_point)
# create a KNN model
knn_model <- nearest_neighbor(neighbors = 3) |>
set_engine('kknn') |>
set_mode('classification')
# fit the KNN model to our data
knn_fit <- knn_model |> fit(classes ~., data = df_juiced)
knn_fitparsnip model object
Call:
kknn::train.kknn(formula = classes ~ ., data = data, ks = min_rows(3, data, 5))
Type of response variable: nominal
Minimal misclassification: 0.1
Best kernel: optimal
Best k: 3# predict new data using the fitted KNN model.
prediction <- predict(object = knn_fit, new_data = df_baked)
new_point_pred <- bind_cols(new_point, prediction) |>
rename(classes = .pred_class)
# Visualize the new prediction
ggplot(data = bind_rows(df, new_point_pred),
aes(x = x, y = y, color = classes)) +
geom_point() +
geom_text(data = new_point_pred,
mapping = aes(label = paste0('new point, class:', new_point_pred$classes)),
nudge_x = 0.9, nudge_y = -0.2)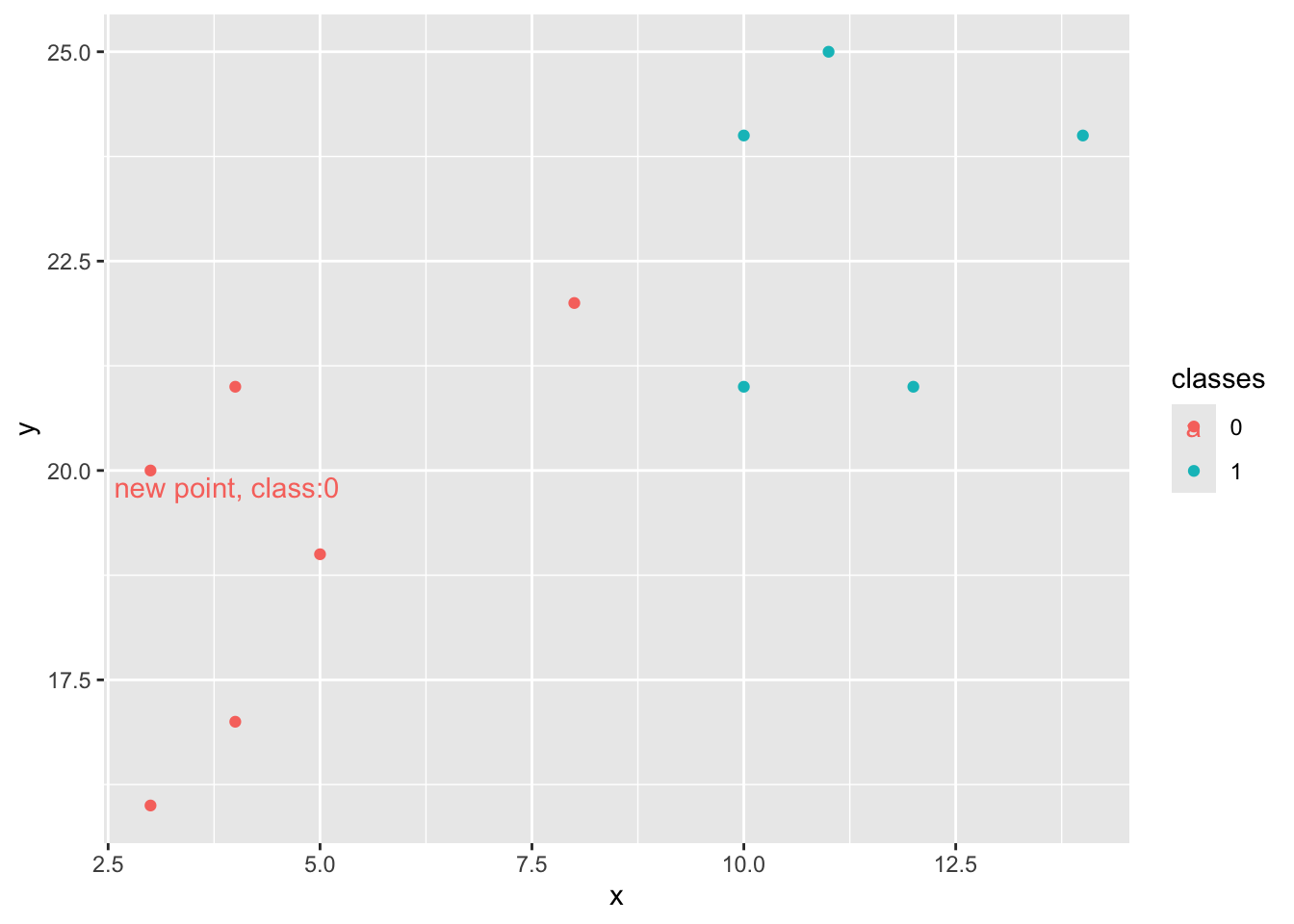
In this example, we create a data set of a 1000 observations (using numbers taken from a normal distribution with a sd of 2.). We’ll make 4 clusters of 250 observations. Because the data comes from a normal distribution, there is no need to scale them this time. We’ll then do a usual split 80-20 % for training and testing set. And we’ll test our data using either K = 5 or K = 19. And then check the accuracy score.
from sklearn.datasets import make_blobs
# create our synthetic data
X, y = make_blobs(n_samples = 1000, n_features = 2,
centers = 4, cluster_std = 2,
random_state = 4)
# visualizing the dataset
plt.scatter(X[:,0], X[:,1], c = y, s = 20)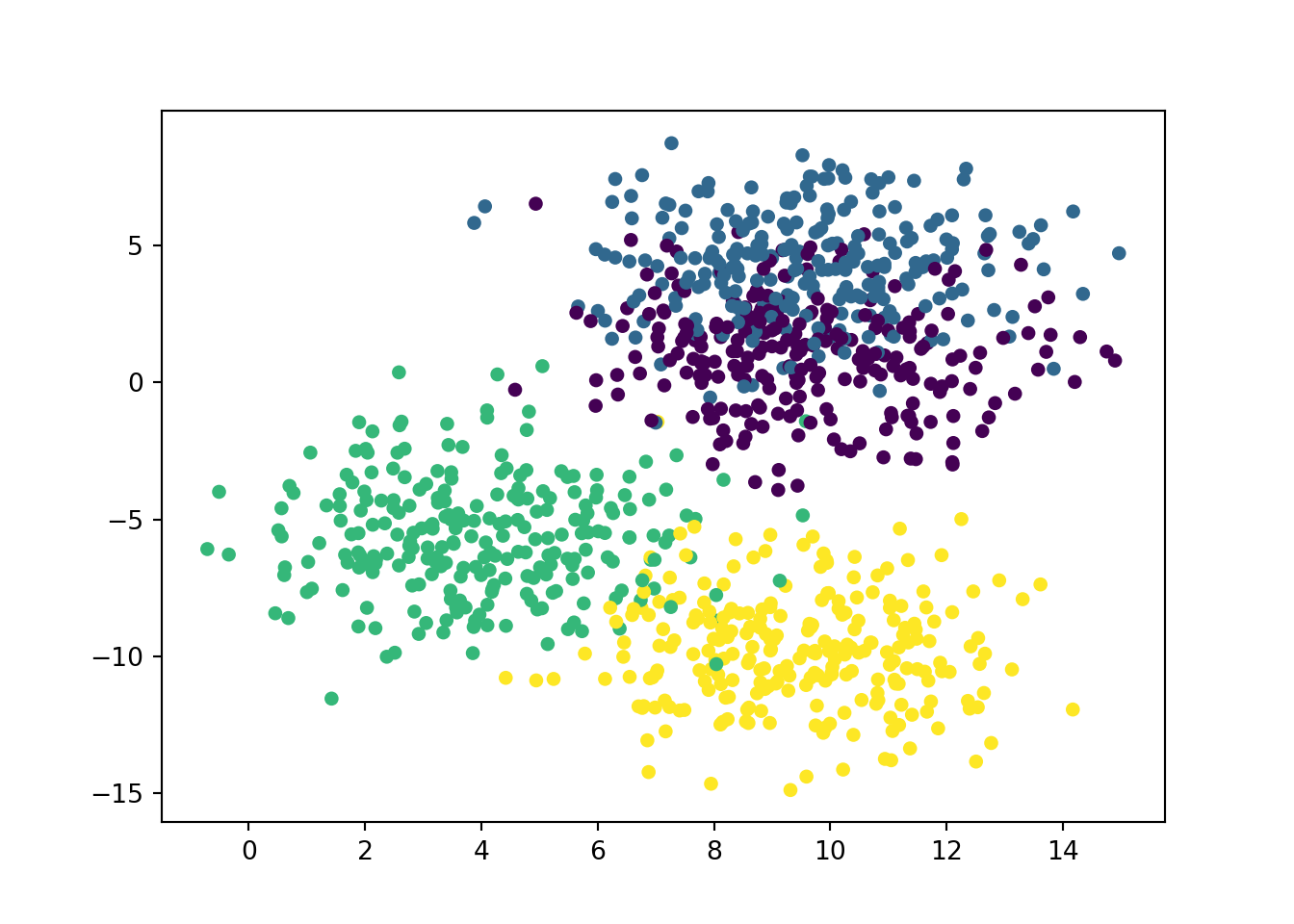
Splitting our data set into training & testing + running KNN on the data
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
# splitting our data into training and testing
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, stratify = y, random_state = 41)
knn5 = KNeighborsClassifier(n_neighbors = 5)
knn19 = KNeighborsClassifier(n_neighbors = 19)
# fit our 'model' with either '5' or '19' Nearest Neighbors
knn5.fit(X_train, y_train)KNeighborsClassifier()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
KNeighborsClassifier()
KNeighborsClassifier(n_neighbors=19)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
KNeighborsClassifier(n_neighbors=19)
# apply prediction on our test set
y_pred_5 = knn5.predict(X_test)
y_pred_19 = knn19.predict(X_test)
from sklearn.metrics import accuracy_score
print('Accuracy with K = 5 is', round(accuracy_score(y_test, y_pred_5)*100, 2), '%')Accuracy with K = 5 is 84.0 %Accuracy with k = 19 is 85.5 %Let’s visualize both ‘models’ and the impact of the choice of K.
#using subplots to compare
plt.figure(figsize = (9, 5))
# first subplot
plt.subplot(1, 2, 1)
plt.scatter(X_test[:, 0], X_test[:, 1], c = y_pred_5, s=20)
plt.title('Predictions with K=5')
# second subplot
plt.subplot(1, 2, 2)
plt.scatter(X_test[:, 0], X_test[:, 1], c = y_pred_19, s=20)
plt.title('Prediction with K=19')
# create our synthetic data
df1 <- tibble(x = rnorm(n = 250, mean = 0, sd = 2) + 4,
y = rnorm(n = 250, mean = 0, sd = 2) - 6,
classes = c(1))
df2 <- tibble(x = rnorm(n = 250, mean = 0, sd = 2) + 9,
y = rnorm(n = 250, mean = 0, sd = 2) - 9,
classes = c(2))
df3 <- tibble(x = rnorm(n = 250, mean = 0, sd = 2) + 9,
y = rnorm(n = 250, mean = 0, sd = 2) + 2,
classes = c(3))
df4 <- tibble(x = rnorm(n = 250, mean = 0, sd = 2) + 10,
y = rnorm(n = 250, mean = 0, sd = 2) + 5,
classes = c(4))
df <- bind_rows(df1, df2, df3, df4) |>
mutate(classes = as.factor(classes))
# visualizing the dataset
ggplot(df, aes(x, y, color = classes)) +
geom_point() +
theme(legend.position = 'none')
This time, we split the data in a training / testing set.
Also because the data were already scaled during the generative process; there is no need to redo that step.
library(rsample)
library(yardstick)
df_split <- initial_split(df, prop = 0.8, strata = classes, )
df_train <- training(df_split)
df_test <- testing(df_split)
#let's first try the ideal model
knn_model_5 <- nearest_neighbor(neighbors = 5) |>
set_engine('kknn') |>
set_mode('classification')
knn_model_19 <- nearest_neighbor(neighbors = 19) |>
set_engine('kknn') |>
set_mode('classification')
knn_fit_5 <- knn_model_5 |> fit(classes ~., data = df_train)
knn5 <- knn_fit_5 |> predict(df_test) |>
bind_cols(df_test) |> mutate(model = 'knn5')
knn5 |> accuracy(truth = classes, estimate = .pred_class)# A tibble: 1 × 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 accuracy multiclass 0.84knn_fit_19 <- knn_model_19 |> fit(classes ~., data = df_train)
knn19 <- knn_fit_19 |> predict(df_test) |>
bind_cols(df_test) |> mutate(model = 'knn19')
knn19 |> accuracy(truth = classes, estimate = .pred_class)# A tibble: 1 × 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 accuracy multiclass 0.87Let’s visualize both ‘models’ and the impact of the choice of K. Note, we have just plotted the predictions, we have not plotted the actual data points used to measure the K nearest observations.
Because the data are already pretty well separated, the only changes we see easily are the ones in the junction between 2 clusters of observations.
This time, we are going to use a stock price to perform KNN.
Loading and checking the data
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('../../../raw_data/AA.csv')
df['date'] = pd.to_datetime(df['date'])
df = df.sort_values(by = 'date', inplace = False)
df.set_index('date', inplace=True)
df.shape(5821, 12) open high low ... vwap label changeOverTime
date ...
2001-01-02 80.50 80.95 76.60 ... 78.35 January 02, 01 -0.0373
2001-01-03 77.50 80.50 75.24 ... 78.10 January 03, 01 0.0135
2001-01-04 78.55 81.25 77.65 ... 80.00 January 04, 01 0.0325
2001-01-05 81.10 81.70 78.85 ... 80.05 January 05, 01 -0.0185
2001-01-08 79.60 85.91 79.00 ... 81.90 January 08, 01 0.0151
[5 rows x 12 columns]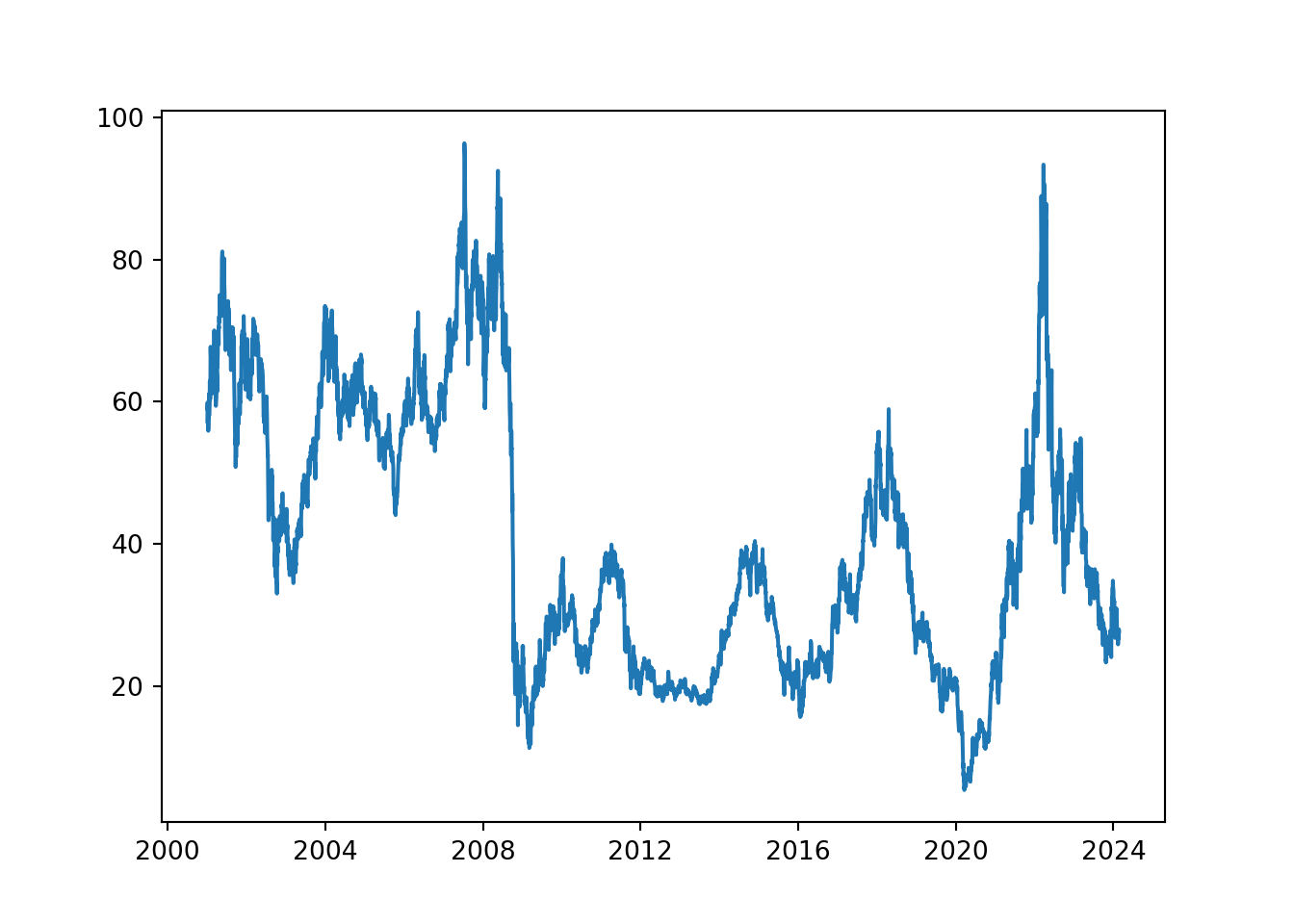
#only keep useful columns
df1a = df.drop(['unadjustedVolume', 'change', 'changePercent', 'vwap', 'label', 'changeOverTime'], axis = 1)
#or easier actually ;-)
#df1b = df.iloc[:, :5]
df1a.describe() open high ... adjClose volume
count 5821.000000 5821.000000 ... 5821.000000 5.821000e+03
mean 46.372343 47.097133 ... 40.404558 6.519558e+06
std 24.755757 25.075361 ... 18.945874 5.452542e+06
min 5.500000 5.950000 ... 5.360000 4.254680e+05
25% 24.990000 25.420000 ... 23.620000 2.656970e+06
50% 38.260000 38.780000 ... 36.270000 5.129900e+06
75% 69.210000 69.980000 ... 56.910000 8.773242e+06
max 115.010000 117.190000 ... 96.360000 1.007518e+08
[8 rows x 6 columns]open 0
high 0
low 0
close 0
adjClose 0
volume 0
dtype: int64No missing values and we can go ahead!
Setting up a few predictors.
import numpy as np
df1a['o_c'] = (df1a['open'] - df1a['close']) / df1a['close']
df1a['h_l'] = (df1a['high'] - df1a['low']) / df1a['close']
df1a['ret_21d'] = np.log(df1a['close'] / df1a['close'].shift(21))
df1a['roll_sd_ret21d_1Y'] = df1a['ret_21d'].rolling(window = 251).std()
df1a['volum_sma200'] = df1a['volume'].rolling(window = 199).mean()
df1a['perc_above_volu_sma200'] = np.log(df1a['volume'] / df1a['volum_sma200'])
df1a['roll_sd_volum_1Y'] = df1a['volume'].rolling(window = 251).std()
df1a['sma50'] = df1a['close'].rolling(window = 50).mean()
df1a['perc_above_sma50'] = np.log(df1a['close'] / df1a['sma50'])
df1a['sma200'] = df1a['close'].rolling(window = 200).mean()
df1a['perc_above_sma200'] = np.log(df1a['close'] / df1a['sma200'])
df1a['roll_corr_sma50_sma200'] = df1a['sma200'].rolling(window = 252).corr(df1a['sma50'])
# setting up a target variable.
# is the stock above 5% in 2 weeks time.
df1a['target'] = np.where(df1a['close'].shift(-41) > 1.015 * df1a['close'], 1, -1)
df1a = df1a.drop(['open', 'high', 'low', 'close', 'adjClose', 'volume', 'sma50', 'sma200', 'volum_sma200'], axis = 1)
df1a = df1a.dropna()
target = df1a['target']
df1a = df1a.drop(['target'], axis = 1)
df1a.shape(5371, 9)Splitting the data set for training and testing. Because time-series and auto-correlation, we won’t randomly take observations from the set for training. Instead, we split in the first 80% of data for training and the last 20% for testing.
from sklearn.model_selection import (train_test_split, GridSearchCV)
x_train, x_test, y_train, y_test = train_test_split(df1a, target, test_size = 0.2, shuffle = False)
print(f"The size for the train and test dataset are {len(x_train)}, {len(x_test)} observations")The size for the train and test dataset are 4296, 1075 observationslibrary(readr)
library(dplyr)
library(ggplot2)
df <- read_csv('../../../raw_data/AA.csv') |>
arrange(date) |>
select(date, open, high, low, close, volume)
ggplot(df, aes(x = date, y = close)) +
geom_line()
# A tibble: 1 × 6
date open high low close volume
<int> <int> <int> <int> <int> <int>
1 0 0 0 0 0 0No missing values, we can go ahead!
Let’s create the predictors.
library(tidyr)
library(timetk)
#defining some rolling functions
mean_roll_50d = slidify(.f = mean, .period = 50, .align = 'right')
mean_roll_107d = slidify(.f = mean, .period = 107, .align = 'right')
mean_roll_199d = slidify(.f = mean, .period = 199, .align = 'right')
sd_roll_19d = slidify(.f = sd, .period = 19, .align = 'right')
sd_roll_31d = slidify(.f = sd, .period = 31, .align = 'right')
sd_roll_1Y = slidify(.f = sd, .period = 251, .align = 'right')
corr_roll_1Y = slidify(.f = ~cor(.x, .y), .period = 251, .align = 'right')
yo <- TTR::aroon(df[, c('high', 'low')], n = 23)
df$aroon <- yo[, 3]
yo <- TTR::CCI(df[, c('high', 'low', 'close')], n = 17)
df$cci <- yo
yo <- TTR::chaikinVolatility(df[, c('high', 'low')], n = 13)
df$chaikinVol <- yo
df1a <- df |>
mutate(o_c = (open - close) / close,
h_l = (high - low) / close,
ret_21d = log(close/lag(close, n = 21)),
roll_sd_ret21d_1Y = sd_roll_1Y(ret_21d),
roll_sd_vol_31d = sd_roll_31d(volume),
sma50 = mean_roll_50d(close),
perc_above_sma50 = log(close / sma50),
sma200 = mean_roll_199d(close),
perc_above_sma200 = log(close / sma50),
sma107_vol = mean_roll_107d(volume),
perc_above_volu_sma107 = log(volume / sma107_vol),
sma200_vol = mean_roll_199d(volume),
perc_above_volu_sma200 = log(volume / sma200_vol),
roll_sd_perc_above_volu_sma200_19d = sd_roll_19d(perc_above_volu_sma200),
roll_corr_sma50_sma200_1Y = corr_roll_1Y(sma50, sma200),
target = as.factor(if_else(lead(close, n =41) > 1.015 * close, 1, -1 ))) |>
select(-open, -high, -low, -close, -volume, -sma50, -sma200,
-sma107_vol, -sma200_vol) |>
drop_na()Let’s now split our training and testing set.
This is when we create the model and create the predictions.
Now we will start building our KNN model using a pipeline or a workflow (for R), First, we need to scale the data then we can go on the classification task.
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import MinMaxScaler
from sklearn.neighbors import KNeighborsClassifier
knn_model = Pipeline([
('scaler', MinMaxScaler()),
('classifier', KNeighborsClassifier())
])
knn_model.fit(x_train, y_train)Pipeline(steps=[('scaler', MinMaxScaler()),
('classifier', KNeighborsClassifier())])In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. Pipeline(steps=[('scaler', MinMaxScaler()),
('classifier', KNeighborsClassifier())])MinMaxScaler()
KNeighborsClassifier()
Go onto predictions
from sklearn.metrics import (ConfusionMatrixDisplay, classification_report)
from sklearn.metrics import (accuracy_score, f1_score)
y_pred = knn_model.predict(x_test)
# or we can also use a probability model
y_pred_proba = knn_model.predict_proba(x_test)
# few checking
knn_model.classes_array([-1, 1])array([[0.8, 0.2],
[1. , 0. ],
[1. , 0. ],
[0.8, 0.2],
[1. , 0. ]])Let’s define a basic model in R using the tidymodel framework.
library(recipes)
library(parsnip)
df_rec <- recipe(formula = target ~., data = df_train) |>
update_role(date, new_role = 'ID') |>
step_scale(all_numeric_predictors())
df_prep <- df_rec |> prep(df_train)
df_juiced <- juice(df_prep)
df_baked <- df_prep |> bake(df_test)
knn_model <- nearest_neighbor() |>
set_mode('classification') |>
set_engine('kknn')
knn_fit <- knn_model |> fit(target ~., data = df_juiced)
knn_pred <- predict(knn_fit, new_data = df_baked)
df_pred <- bind_cols(df_baked |> select(date, target), knn_pred) precision recall f1-score support
-1 0.47 0.69 0.56 542
1 0.39 0.21 0.27 533
accuracy 0.45 1075
macro avg 0.43 0.45 0.41 1075
weighted avg 0.43 0.45 0.42 1075# checking accuracy and f1
acc_train = accuracy_score(y_train, knn_model.predict(x_train))
acc_test = accuracy_score(y_test, knn_model.predict(x_test))
f1_test = f1_score(y_test, knn_model.predict(x_test))
print(f"Accuracy for training set is {acc_train:0.3} and Accuracy for testing set is {acc_test:0.3}")Accuracy for training set is 0.928 and Accuracy for testing set is 0.449f1 score for test set is 0.271# A tibble: 2 × 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 accuracy binary 0.507
2 kap binary 0.0189# A tibble: 1 × 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 f_meas binary 0.539# A tibble: 1 × 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 precision binary 0.491We can always try to fine tune our KNN algorithm to see if we can get a better result on our test set.
Let’s find the best parameters through a grid search
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import roc_auc_score, auc
knn_model.get_params(){'memory': None, 'steps': [('scaler', MinMaxScaler()), ('classifier', KNeighborsClassifier())], 'verbose': False, 'scaler': MinMaxScaler(), 'classifier': KNeighborsClassifier(), 'scaler__clip': False, 'scaler__copy': True, 'scaler__feature_range': (0, 1), 'classifier__algorithm': 'auto', 'classifier__leaf_size': 30, 'classifier__metric': 'minkowski', 'classifier__metric_params': None, 'classifier__n_jobs': None, 'classifier__n_neighbors': 5, 'classifier__p': 2, 'classifier__weights': 'uniform'}param_grid = {'classifier__n_neighbors': np.arange(2, 51, 1)}
gs = GridSearchCV(knn_model, param_grid,
scoring = 'f1', n_jobs = -1,
cv = tscv,
verbose = 1)
gs.fit(x_train, y_train)GridSearchCV(cv=TimeSeriesSplit(gap=10, max_train_size=None, n_splits=10, test_size=None),
estimator=Pipeline(steps=[('scaler', MinMaxScaler()),
('classifier', KNeighborsClassifier())]),
n_jobs=-1,
param_grid={'classifier__n_neighbors': array([ 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18,
19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35,
36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50])},
scoring='f1', verbose=1)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. GridSearchCV(cv=TimeSeriesSplit(gap=10, max_train_size=None, n_splits=10, test_size=None),
estimator=Pipeline(steps=[('scaler', MinMaxScaler()),
('classifier', KNeighborsClassifier())]),
n_jobs=-1,
param_grid={'classifier__n_neighbors': array([ 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18,
19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35,
36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50])},
scoring='f1', verbose=1)Pipeline(steps=[('scaler', MinMaxScaler()),
('classifier', KNeighborsClassifier(n_neighbors=np.int64(9)))])MinMaxScaler()
KNeighborsClassifier(n_neighbors=np.int64(9))
print(f"Optimal Neighbours: {gs.best_params_['classifier__n_neighbors']}, Best, Score: {round(gs.best_score_,4)}")Optimal Neighbours: 9, Best, Score: 0.3128Let’s now use the best parameter found for our model.
from sklearn.metrics import f1_score
tuned_knn_model = KNeighborsClassifier(n_neighbors = gs.best_params_['classifier__n_neighbors'])
tuned_knn_model.fit(x_train, y_train)KNeighborsClassifier(n_neighbors=np.int64(9))In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
KNeighborsClassifier(n_neighbors=np.int64(9))
Using the tidymodel framework, when it comes to hyperparameters tuning, we then use a workflow to structure all the work for us.
library(rsample)
library(workflows)
library(tune)
library(dials)
library(yardstick)
# create the CV validation resampls
tscv = rolling_origin(df_train, initial = 1200, assess = 100, lag = 20, skip = 300, cumulative = T)
# create the KNN model with leaving hyperparameters for tuning
knn_model_tuned <- nearest_neighbor(neighbors = tune(),
weight_func = tune(),
dist_power = tune()) |>
set_mode('classification') |>
set_engine('kknn')
# create a grid with different values for the hyperparamter
nn_grid <- grid_regular(neighbors(range = c(2, 51)),
weight_func(), dist_power(range = c(0.12, 2)),
levels =6)
knn_param = parameters(neighbors(range = c(5, 51)), weight_func(),
dist_power(range = c(0.12, 2)))
nn_grid_maxEnthropy = grid_max_entropy(knn_param, size = 150)
# create a workflow that will bring all steps together.
knn_wf <- workflow(preprocessor = df_rec, spec = knn_model_tuned)
# fitting the models for the various hyperparameters
library(doParallel)
registerDoParallel()
knn_fit <- tune_grid(knn_wf, resamples = tscv,
metrics = metric_set(accuracy, f_meas, roc_auc),
control = control_resamples(save_pred = T, verbose = T),
grid = nn_grid_maxEnthropy)
metrics <- knn_fit |> collect_metrics() |>
arrange(.metric, desc(mean))
# another cool trick with collecting predictions for all the models.
all_pred <- knn_fit |> select(.predictions) |> unnest(cols = c(.predictions))
# now we need to decide which is the 'best' model
# we say the best model is the one that has the best f1 score
best_knn_model = knn_fit |> show_best(metric = 'f_meas', n =1)
best_knn_model# A tibble: 1 × 9
neighbors weight_func dist_power .metric .estimator mean n std_err
<int> <chr> <dbl> <chr> <chr> <dbl> <int> <dbl>
1 7 biweight 1.82 f_meas binary 0.667 10 0.0424
# ℹ 1 more variable: .config <chr>Warning in mtr_info$metric == metric: longer object length is not a multiple of
shorter object length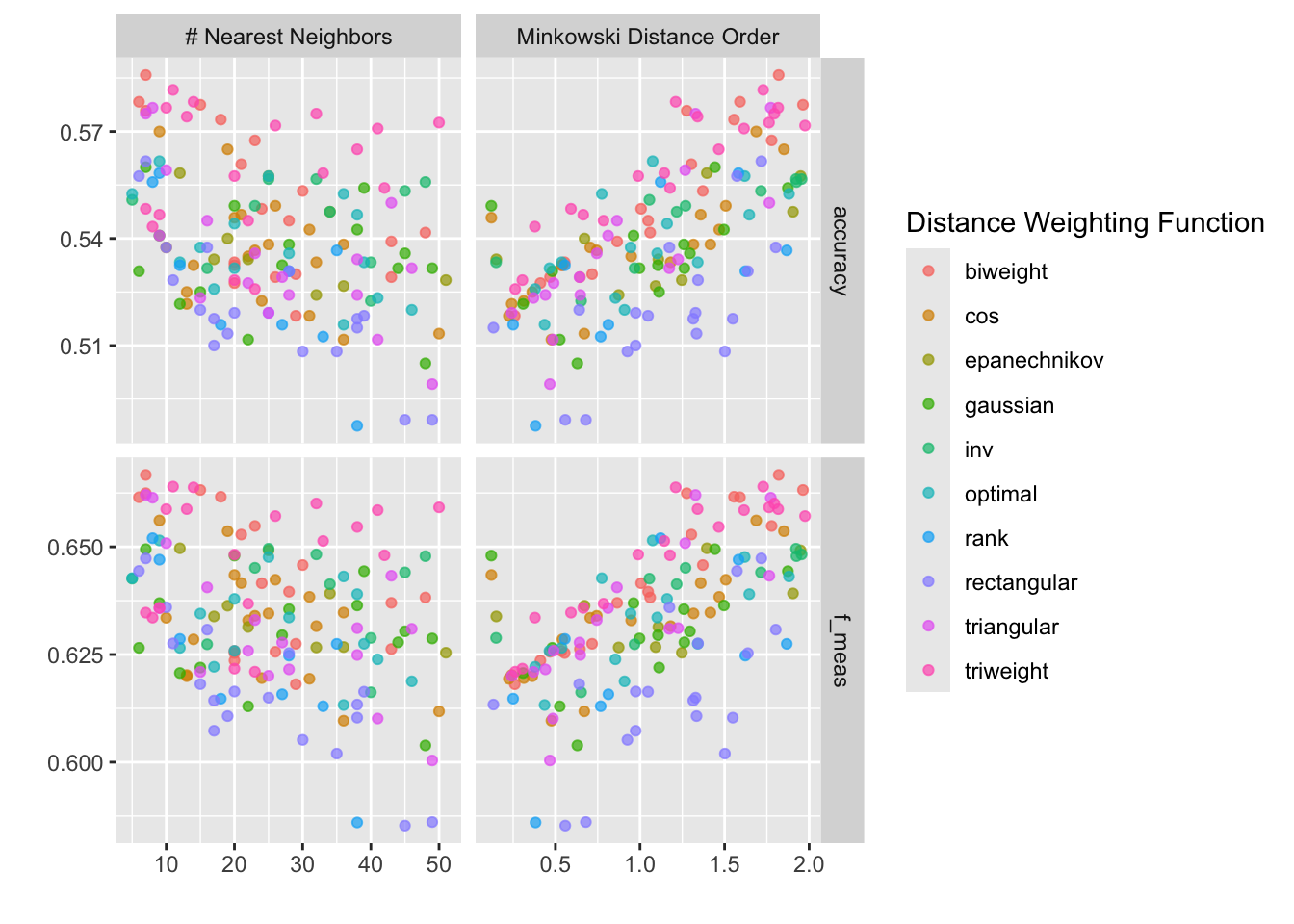
We can fit the best model (the one with the parameters that gives the best f1 score) as the final model. Then we’ll make prediction using that model
acc_train = accuracy_score(y_train, tuned_knn_model.predict(x_train))
acc_test = accuracy_score(y_test, y_pred_tuned)
f1_test = f1_score(y_test, y_pred_tuned)
print(f'\n Training Accuracy \t: {acc_train :0.4} \n Test Accuracy \t\t: {acc_test :0.4}')
Training Accuracy : 0.8119
Test Accuracy : 0.5014
Test f1 score : 0.4136df_pred <- bind_cols(df_baked |> select(date, target), knn_pred)
df_pred |> metrics(target, .pred_class)# A tibble: 2 × 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 accuracy binary 0.503
2 kap binary 0.0113# A tibble: 1 × 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 f_meas binary 0.534# A tibble: 1 × 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 precision binary 0.488We can then check a trading strategy based on that model.
df1 = df1a.copy()
df1['signal'] = tuned_knn_model.predict(df1)
df['returns'] = np.log(df['close']).diff(41).fillna(0)
df2 = df[['close', 'returns']]
yo = df1.merge(df2, left_index = True, right_index = True, how = 'left')
df1 = yo
df1['strategy'] = df1['returns'] * df1['signal'].shift(41).fillna(0)
df1.index = df1.index.tz_localize('utc')